Скрытые Марковские модели в распознавании речи
Самое быстрое и эффективное взаимодействие между людьми происходит посредством устной речи. С помощью речи могут быть переданы различные чувства и эмоции, а главное — полезная информация. Необходимость создания компьютерных интерфейсов звукового ввода-вывода не вызывает сомнений, поскольку их эффективность основана на практически неограниченных возможностях формулировки в самых различных областях человеческой деятельности.
Первая электронная машина, синтезирующая английскую речь, была представлена в Нью-Йорке на торговой выставке в 1939 году и называлась voder, но звук, который она воспроизводила, был крайне нечетким. Первое же устройство для распознавания речи вышло в свет в 1952 втором году и было способно распознавать цифры.
При процессе распознавания речи можно выделить следующие сложности: произвольный, наивный пользователь; спонтанная речь, сопровождаемая аграмматизмами и речевым «мусором»; наличие акустических помех и искажений; наличие речевых помех.
Из всего многообразия методов в данной статье мы рассмотрим возможность создания статистической модели посредством скрытых Марковских моделей (СММ).
Part-Of-Speech tagging
При анализе естественного языка первым шагом необходимо определить: к какой части речи относится каждое из слов в предложении. В английском языке задача на этом этапе называется Part-Of-Speech tagging. Каким образом мы можем определить часть речи отдельного члена предложения? Рассмотрим предложение на английском языке: «The can will rust». Итак, the –определенный артикль или частица «тем»; can – может одновременно являться и модальным глаголом, и существительным, и глаголом; will – модальный глагол, существительное и глагол; rust – существительное или глагол. В статистическом подходе необходимо построить таблицу вероятностей использования слов в каждом грамматическом значении. Эту задачу можно решить на основе тестовых текстов, проанализированных вручную. И сразу можно выделить одну из проблем: слово «can» в большинстве случаев используется в качестве глагола, но иногда оно может являться и существительным. Учитывая этот недостаток, была создана модель, принимающая во внимание тот факт, что после артикля последует прилагательное или существительное:
Где:
t – таг (существительное, прилагательное и т.д.)
w – слово в тексте (rust, can …)
p(w|t) – вероятность того, что слово w соответствует тагу t
p(t1|t2) – вероятность того, что t1 идет после t2
Из предложенной формулы видно, что мы пытаемся подобрать таги так, чтобы слово подходило тагу, и таг подходил предыдущему тагу. Данный метод позволяет определить, что «can» выступает в роли существительного, а не как модального глагола.
Эта статистическая модель может быть описана как эргодическая СММ: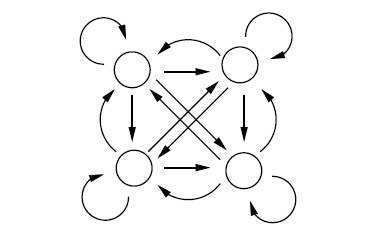
Эргодическая Марковская модель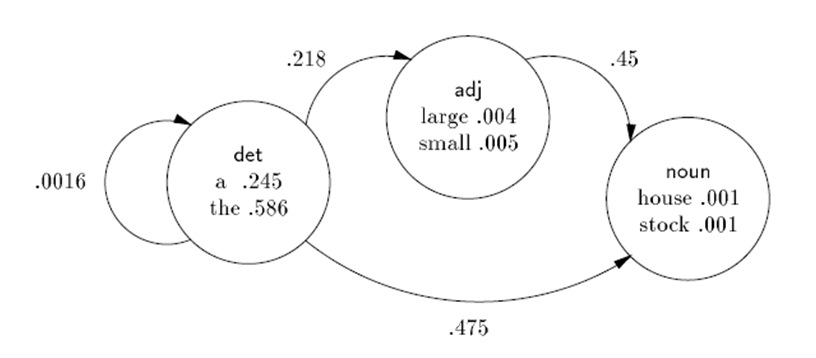
Эргодическая Марковская модель на практике
Каждая вершина в данной схемы обозначает отдельную часть речи, в которой записываются пары (слово; вероятность, что слово относится именно к этой части речи). Переходы показывают возможную вероятность следования одной части речи за другой. Так, например, вероятность того, что подряд будут идти 2 артикля, при условии, что встретится артикль, будет равна 0,0016. Данный этап распознавания речи очень важен, так как правильное определение грамматической структуры предложения позволяет подобрать верную грамматическую конструкцию для экспрессивной окраски воспроизводимого предложения.
N-граммные модели
Также существуют n-граммные модели распознавания речевого потока. Они основаны на предположении, что вероятность употребления очередного слова в предложении зависит только от n-1 слов. Сегодня наиболее популярные биграммные и триграммные модели языка. Поиск в таких моделях происходит по большой таблице (корпусу). Несмотря на быстро работающий алгоритм, такие модели не способны уловить семантические и синтаксические связи, если зависимые слова находятся на расстоянии 5 слов друг от друга. Использование же n-граммных моделей, где n больше чем 5, требует огромных мощностей.
Как уже отмечалось выше, самой популярной моделью на сегодняшний день является триграммная модель. Условная вероятность наблюдения предложения w1, … wn приближена к:
P(w1,…,wn) = ΠP(wi | w1,…,w2) ≈ ΠP(wi | wi-(n-1), …, wi-1)
Например, рассмотрим предложение «I want to go home». Вероятность этого предложения можно вычислить от счета частоты n-грамма (в этом примере возьмем n=3):
P(I, want, to, go, home) ≈ P(I)*P(want|I)*P(to|I, want)*P(go|want, to)*P(home| to, go)
Стоит отметить, дальнодействующую триграммную модель, в которой анализ ведется не только по двум предшествующим словам, а по любой паре слов, находящихся рядом. Такая триграммная модель может пропускать малоинформативные слова, тем самым улучшая предсказуемость сочетаемости в модели.
Обратная связь
Интересуют вопросы реализации алгоритмов, программирования, выбора электроники и прочая информация, постараюсь осветить в отдельных статьях
пишите мне на netdm@mail.ru


Добавить комментарий